내적

한 벡터를 다른 벡터에 정사영시켜 그 힘의 값을 얻는 공식
a라는 줄을 b의 방향으로 당길때 발생하는 힘

v1과 v2를 내적하는 공식
v1 (a, b, c)
v2 (k, h, w)
a*k + b*h + c*w
=
v1 벡터의 크기 * v2 벡터의 크기 * cos세타
fabs(sqrt(a*a + b*b + c*c)) * fabs(sqrt(k*k + h*h + w*w)) * cos(r)
위 배경지식을 이용해 본 문제를 해결해보자.
본 문제는 리그오브레전드의 애쉬 스킬에 피격당하는 적을 판별하고 리스트에 담아서 리턴하는 문제이다.
그래프로 표현해보면 다음과 같다.
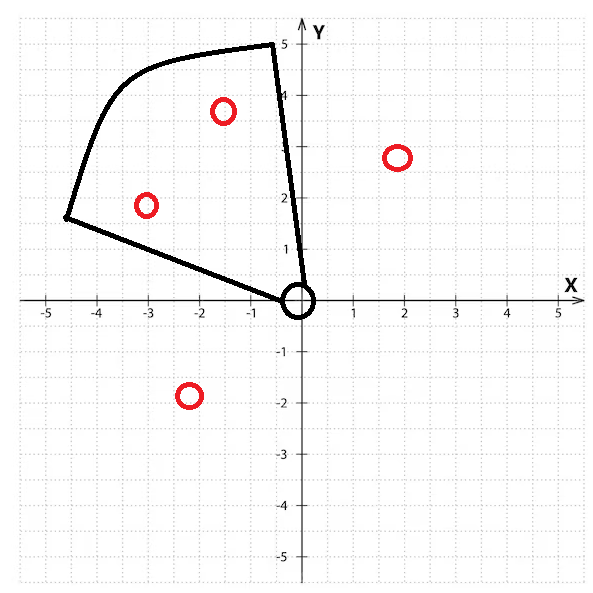
문제:
부채꼴 범위의 스킬을 사용하는 캐릭터가 있다
부채꼴 범위에 있다면 무조건 피격당하며
아닌 경우 피격당하지 않는다.
이때 피격을 당하는 객체를 백터리스트에 담아 리턴하라
조건1 : 스킬을 사용하는 게임 캐릭터는 항상 0,0 위치에 있습니다.
조건2 : 적들은 0,0에 있을 수 없으며, 겹쳐있지 않습니다.
조건3 : 캐릭터와 일직선상에 적이 2명 이상 겹쳐있어도, 범위 안에만 들어오면 다 데미지를 받는 것으로 인식합니다.
주어지는 값
스킬 마우스 좌표 mx, my
적의 위치 리스트 vector<vector<int>> targets;
부채꼴 각도 int d
스킬의 반지름 int r
알고리즘 순서
1. 부채꼴 반지름 내에 없으면 목록에서 피격 제외한다.
2. 내적을 이용해 부채꼴의 라디안 값을 구한다.
3. 루프를 돌면서 피격체의 라디안 값이 부채꼴의 라디안 값보다 크면 제외한다.
4. 남은 피격체의 리스트를 리턴한다.
#include <vector>
#include <cmath>
#define PI 3.141592
// 거리 및 벡터 크기
double Distance(int a, int a)
{
return sqrt(a*a + b*b);
}
// 내적
int Dot_Product(int a1, int b1, int a2, int b2)
{
return a1 * a2 + b1 * b2;
}
int main(vector<int> mouse,
double distance, int degree, vector<vector<int>> targets)
{
int nCount = 0;
// 부채꼴의 라디안 값 1/2
double radian = (degree / 2) * (PI / 180.0);
// 마우스 벡터의 크기
double mouseVsize = Distance(mouse[0], mouse[1]);
for (auto& target : targets)
{
if (Distance(target[0], target[1]) > distance) // 거리 비교
continue;
else
{
// 내적 값
int dot = Dot_Product(mouse[0], mouse[1], target[0], target[1]);
// 타겟의 벡터 사이즈
double targetVsize = Distance(target[0], target[1]);
// 내적을 이용한 라디안 값 얻어오기
double theta = acos(dot / (targetVsize * radian));
// 만약 부채꼴의 각도보다 작으면 피격
if (theta <= radian)
++nCount;
}
}
return nCount;
}'CS > 알고리즘' 카테고리의 다른 글
| 퀵 정렬(quick sort) 알고리즘 (2) | 2023.12.28 |
|---|---|
| 재귀_동적_프로그래밍 (0) | 2021.03.01 |
| 수와 표현 (0) | 2021.02.28 |
| 논리증명 (0) | 2021.02.28 |